What is Gradient Descent?
Gradient Descent is an optimization algorithm used in machine learning to minimize a loss function by iteratively adjusting model parameters. It helps improve model accuracy by reducing the difference between predicted and actual values.
How Does Gradient Descent Work?
Gradient Descent operates through an iterative process that seeks to find the minimum of a loss function. Here’s how it functions:
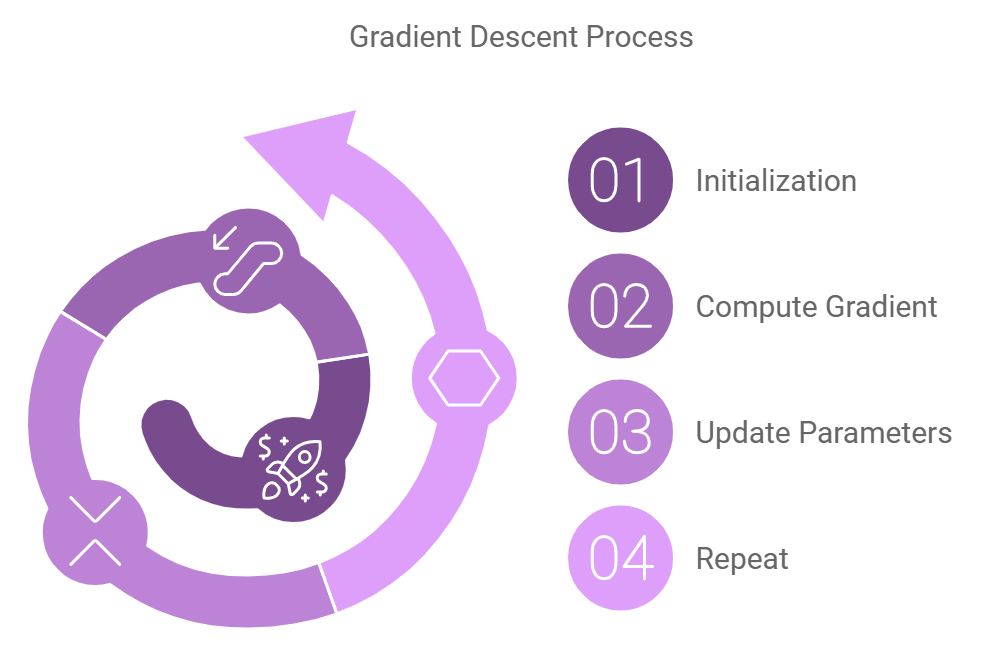
- Initialization: Start with an initial guess for the model parameters.
- Compute Gradient: Calculate the gradient of the loss function concerning each parameter to determine the direction of the steepest ascent.
- Update Parameters: Adjust the parameters in the opposite direction of the gradient (steepest descent) using a learning rate, which controls the step size.
- Repeat: Iterate this process until the loss function converges to its minimum or the changes in parameters are negligible.
Types of Gradient Descent:
- Batch Gradient Descent: Processes the entire dataset in one iteration, leading to stable convergence but high computational cost.
- Stochastic Gradient Descent (SGD): Processes one data point per iteration, offering faster updates but higher variability.
- Mini-Batch Gradient Descent: Combines the advantages of both by processing small batches of data at each iteration.
Key Techniques in Gradient Descent Optimization:
- Momentum: Speeds up convergence by adding a fraction of the previous update to the current update.
- Adaptive Learning Rates: Methods like Adam and RMSprop dynamically adjust learning rates for better optimization.
Common Uses and Applications of Gradient Descent
Gradient Descent is foundational in optimizing machine learning models and is applied across various domains:
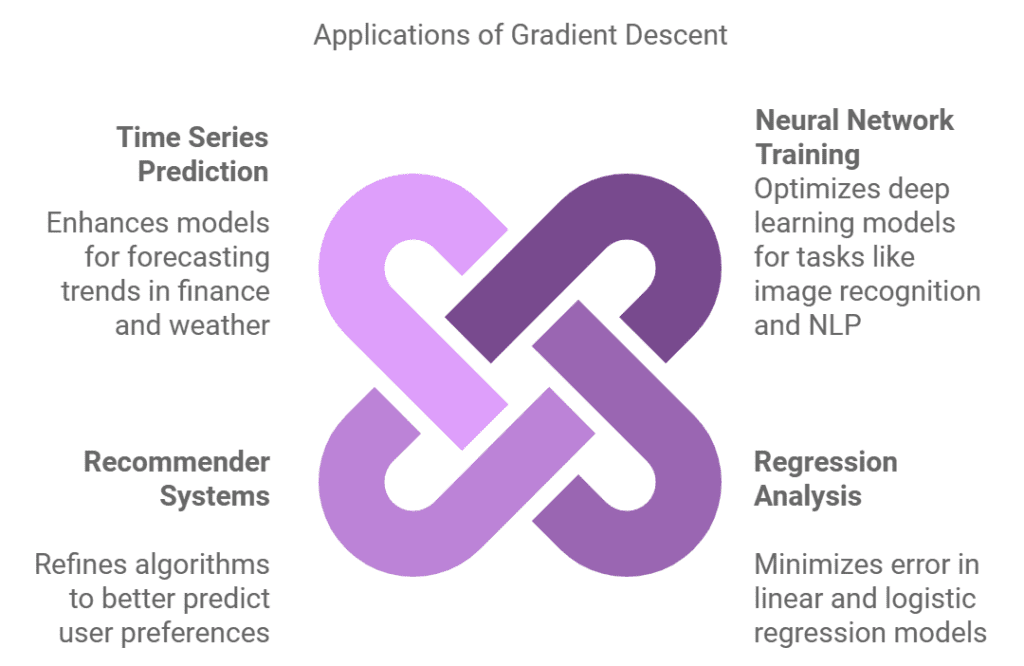

- Neural Network Training: Optimizes deep learning models for image recognition, NLP, and more.
- Regression Analysis: Minimizes error in linear and logistic regression models.
- Recommender Systems: Refines algorithms to better predict user preferences.
- Time Series Prediction: Enhances models for forecasting trends in finance, weather, and other fields.
Advantages of Gradient Descent
Gradient Descent offers numerous benefits:
- Efficiency: Enables scalable optimization for large datasets and complex models.
- Flexibility: Works with a wide range of machine learning algorithms, including neural networks and regression models.
- Adaptability: Can be tailored through advanced techniques like momentum and adaptive learning rates to suit specific tasks.
Drawbacks or Limitations of Gradient Descent
While Gradient Descent is powerful, it has some limitations:
- Local Minima: The algorithm can get stuck in local minima, especially for non-convex loss functions.
- Computational Cost: Training on large datasets or complex models can be resource-intensive.
- Learning Rate Sensitivity: Choosing an inappropriate learning rate can lead to slow convergence or divergence.
Real-Life Examples of Gradient Descent in Action
For example, Gradient Descent is used by deep learning frameworks like TensorFlow and PyTorch to train neural networks for applications such as facial recognition and speech synthesis. This demonstrates its importance in improving the performance of AI systems.
How Does Gradient Descent Compare to Similar Concepts?
Compared to other optimization algorithms, such as Newton’s Method, Gradient Descent is computationally simpler and more suitable for high-dimensional problems. While Newton’s Method provides faster convergence, it is resource-intensive and less practical for large-scale applications.
Future Trends in Gradient Descent
Future advancements in Gradient Descent are likely to focus on:

- Hybrid Approaches: Combining gradient-based optimization with evolutionary algorithms for better convergence.
- Enhanced Scalability: Developing algorithms that handle increasingly large datasets and models.
- Real-Time Training: Adapting techniques for streaming data and dynamic environments.
Best Practices for Using Gradient Descent
To use Gradient Descent effectively, it is recommended to:
- Select the Right Variant: Choose between batch, stochastic, or mini-batch gradient descent based on dataset size and computational resources.
- Optimize Learning Rate: Employ techniques like learning rate schedules or adaptive optimizers (e.g., Adam).
- Monitor Convergence: Use validation loss and metrics to ensure the algorithm is progressing effectively.
Case Studies: Successful Implementation of Gradient Descent
One notable example is the use of Gradient Descent in Google’s AlphaGo project. By leveraging gradient-based optimization, AlphaGo achieved exceptional performance in complex decision-making scenarios, such as the board game Go.
Related Terms to Understand Gradient Descent
- Optimization Algorithm: Algorithms that minimize or maximize a function by adjusting input parameters.
- Learning Algorithm: Refers to methods used to train machine learning models.
- Gradient-Based Optimization: Techniques that rely on gradients for improving model performance.
Steps to Implement Gradient Descent
- Define the loss function to be minimized.
- Choose an initial set of parameters.
- Compute the gradient of the loss function with respect to parameters.
- Update parameters using the learning rate and gradient direction.
- Iterate until convergence or performance goals are met.
By following these steps, you can effectively train models using Gradient Descent.
FAQs
Q: What is Gradient Descent used for?
A: Gradient Descent is used to optimize machine learning models by minimizing the loss function during training.
Q: What are the types of Gradient Descent?
A: Batch Gradient Descent, Stochastic Gradient Descent (SGD), and Mini-Batch Gradient Descent are the main types.
Q: How do learning rates impact Gradient Descent?
A: The learning rate determines the step size during optimization. Too high a rate can cause divergence, while too low a rate results in slow convergence.
Q: What challenges exist in Gradient Descent?
A: Challenges include selecting the appropriate learning rate, avoiding local minima, and managing computational costs for large datasets.